|
 |
 |
 |
חזרה3 |
מוזיקה, שרבים תופשים אותה כאמנות הנעלה והשמימית ביותר, קשורה קשר הדוק למתמטיקה ולמספרים, בעיקר כשמדובר בסולמות המוזיקליים השונים ובהרמוניות. מעט על הקשר שבין מלכת המדעים למלכת האמנויות
מה למתמטיקה ולמוזיקה? האם עולם התחושות והחוויות הנפרש בתודעתנו בעת שאנו מאזינים ל"תשיעית" של בטהובן, או לקטע ג'אז, ניתן לאיפיון, ולוּ באופן חלקי, על ידי מספרים, בדומה למציאות הפיזיקלית? פיתגורס, שחי ביוון הקדומה לפני כ-2500 שנה היה הראשון שהצביע על הקשר בין צלילים ומספרים. הוא הראה כי צירופי צלילים ערֵבים לאוזן – הרמוניות מוזיקליות – התקבלו בכלֵי מיתר כאשר יחסי האורך בין המיתרים היו כיחס פשוט בין שני מספרים שלמים. כך, למשל, שני מיתרים העשויים מאותו חומר ובעלי אותו העובי מפיקים צלילים דומים מאד מבחינה מוזיקלית, שהמרווח ביניהם הוא אוקטבה (ראו להלן), כאשר יחס האורכים בין המיתרים הוא 11:2. יתכן שתוצאה זו חיזקה בלבו את השערתו ש"הכל מִסְפר", כלומר שכל תופעה טבעית ואף אנושית ניתנת להצגה מלאה בעזרת יחסים פשוטים בין מספרים. חלק מהשימושים שהציע למספרים נראה לנו כיום מוזר מאד. כך, למשל, סבר שהמספר 4 מסמל את הגבר וגם את ניגודו – האִשה. בין תלמידיו, הפיתגוראים, היו שטענו שכוכבי הלכת משמיעים את "ההרמוניות השמימיות" (ההרמוניות של הספֵירות) בעת תנועתם במסילותיהם, אלא שאנו איננו מודעים למוזיקה מופלאה זו משום שאנו שומעים אותה מרגע לידתנו2.
 |
מתנודות אוויר לתנודות-נפש |
חקר ההרמוניות בין הצלילים השונים שימש במהלך הדורות כאמצעי לבניית הסולם המוזיקלי שצליליו הם אבני הבניין של השפה המוזיקלית. שפה זו נשגבת יותר מהשפה המילולית, כך סבר הפילוסוף ז'אן-ז'ק רוסו, לא רק משום שהיא מאפשרת תקשורת רגשית עמוקה יותר בין יוצר המוזיקה למאזין, אלא גם בשל היסודות המתמטיים המאפיינים אותה3. כלומר, היא הרבה יותר אנליטית משפת הדיבור, מאחר שהיחסים שבין היסודות הבסיסיים ביותר שבה – הצלילים, הם יחסים מספריים פשוטים.
כאשר כלי נגינה מפיק צליל מסוים, הוא גורם לרטט האוויר המקיף אותו. תנודות אלו מועברות בצורת גלי לחץ דרך האוויר, עד אשר הן מגיעות לאוזנינו וגורמות לרטיטת "עור התוף" המקשר בין האוזן החיצונית לאוזן התיכונה. רטט עור התוף הופך לזעזועים מכאניים בעצמות השמע הזעירות, זעזועים הגורמים תנודות בנוזל שבאוזן הפנימית. תנודות נוזל זה גורמות לתנודות של שכבת תאי חוש השמע שב"שבלול" האוזן הפנימית. כל אזור לאורך פיתוליו של השבלול יכול לרטוט בתדר מסוים. רטט זה גורם לעיוות מחזורי של שלוחות מיקרוסקופיות של תאי חוש השמע, שלוחות המכונות "שערות". העיוות המחזורי של ה"שערות" הללו גורם שינויים חשמליים בתאי חוש השמע, שינויים המתבטאים בהפרשה של שליח-עצבי (נוירוטרנסמיטר), המפעיל את סיבוֹני עצב השמע, ואלה מעבירים את המידע למרכזי השמיעה שבמוח. מרכזים אלה מפענחים כקולות את האותות העצמים המגיעים אליהם, ומפענחים בהם צלילים, מוזיקה ומילים, ומקשרים זאת לתחושות ולחוויות.
התהליכים המוחיים האלה טרם פוענחו כל צורכם, והתחום הידוע כפסיכו-מוזיקה לוט באי-ידיעה. לעומת זאת, אנו יודעים לתאר באופן איכותי וכמותי את התהליכים הפיזיקליים החל מרגע יצירת הצליל בכלי הנגינה ועד הגעת התנודות החשמליות למרכזי השמיעה. מסתבר שחלק מתחושות ההנאה מהמוזיקה שאנו שומעים, בייחוד אלו הקשורות לסולם הצלילים, להרמוניות המוזיקליות, לסטרוקטורות של היצירות המוזיקליות ולמודולציות (מעברים מסולם אחד לשני ביצירה המוזיקלית) ניתן להסביר על בסיס מתמטי, על-פי התיאור הכמותי של הצלילים.
 |
צירופים ערֵבים זה לזה |
את הצלילים – אבני הבניין של השפה המוזיקלית, ניתן לאפיין באופן כמותי מדויק על ידי מספר תכונות: משך, עוצמה, גובה (pitch), וגוון. משך הזמן הבסיסי במוזיקה, שנהוג לכנותו "שלם", ניתן לחלוקה, על פי קצב היצירה, למספר שונה של חלקים. כך, למשל, אם בכל שלם יש 4 צלילים שווים מבחינת משך, אומרים שקצב המוזיקה הוא "ארבעה רבעים" 4/4, ואם השלם מחולק ל-3 צלילים בעלי אותו משך – הקצב מכונה 3/4 . קיימים, כמובן, קצבים מסובכים יותר. עוצמת הצליל גם היא ניתנת לכימות – עוצמת הצליל קשורה לשינוי בלחץ האוויר שיוצר גל הקול, אלא שהמוזיקאים אינם משתמשים בתיאור מִספרִי מדויק לעוצמת הצליל ביצירותיהם, ובמקום זאת הם משתמשים במילים כגון "חלש" (Piano) או "חזק" (Forte). ואולם, האופי המתמטי הבולט ביותר בתורת הצלילים קשור לגובה הצליל ולגוון שלו.
גובה הצליל קשור לתדר (Frequency) של גל הקול, כלומר למספר הפעמים שגל זה רוטט בשניה (יחידת התדר היא "הֶרץ"' – תנודה אחת בשניה). ככל שתדר הגל גבוה יותר כן הצליל גבוה יותר. כך למשל הצליל "לָה" (A) המרכזי בפסנתר מתאים לגל קול הרוטט בתדר 440 תנודות לשניה (440 הֶרץ). גלי הקול נוצרים כתוצאה של רטט מיתרי-הקול שבגרון (וראו: קטיס ריסט – "שרירי שירה", גליליאו 39), מיתרים בכלי מיתר, קרומיות (מֶמברנות) בכלי הקשה.
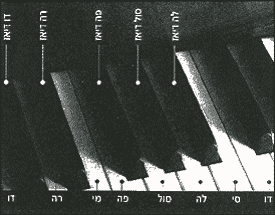
כאשר משמיעים בה-בעת מספר צלילים שונים, נוכחים לדעת שלעתים צירוף הצלילים נעים מאד לאוזן – ואז אנו אומרים שצירוף הצלילים מהווה קונסוננס, או צירוף הַרמוֹני. אך במקרים רבים צירוף הצלילים אינו ערב לאוזן, ובמקרה זה אנו אומרים שהוא מהווה צירוף לא-הרמוני, או דיסוננס. מהי התכונה הקובעת האם צירוף מסוים של 4 צלילים הוא הרמוני או לא? מסתבר שניתן לתת לשאלה זו תשובה כמותית ברורה. צירוף צלילים הרמוני כאשר יחס התדרים של גלי הקול המתאימים לצלילים הללו הוא יחס מספרי פשוט, כלומר יחס בין שני מספרים שלמים קטנים. ככל שהמספרים השלמים בהם מדובר קטנים יותר, צירוף הצלילים ערב יותר לאוזן. למשל, יחס 2:1 מגדיר שני צלילים שהמרחק ביניהם מכונֶה בשפת המוזיקה "אוקטבה" (אוקטבה – מלשון 8) מכיוון שהם מרוחקים זה מזה 8 טונים, למשל, מדוֹ נמוך ל-דו גבוה יותר. אם נשמיע יחד צליל מסוים ואת האוקטבה שלו נקבל את ההרמוניה הטובה ביותר. למעשה שני צלילים כאלה נשמעים לאוזן מאד דומים זה לזה. כך למשל אם ננגן את הצליל "לָה" המרכזי בפסנתר, המתאים לתדר 440 הרץ, ומיד לאחריו את הצליל "לה" הגבוה ממנו באוקטבה (המתאים לתדר כפול, 880 הרץ), שני הצלילים ישמעו כמעט זהים זה לזה.
צירוף שני צלילים שיחס התדרים ביניהם הוא 3:2, כלומר שתדר הצליל האחד גבוה פי 3/2 מהשני, גם הוא ערב מאד לאוזן. צלילים כאלה מרוחקים זה מזה במקלדת הפסנתר ב-7 חצאי טונים. אם נשמיע יחד את הצלילים "דו" ו-"סול" הצירוף ישמע הרמוני כי יחס התדרים בין שני צלילים אלה הוא כיחס המספרים 3/2, כלומר, תדר הצליל "סול" גבוה פי 3/2 מתדר הצליל "דו" (המרחק בין 2 צלילים אלה הוא 7 חצאי טונים). הדבר נכון גם ביחס לצמד הצלילים "מי" ו-"סי" (תוכלו להיווכח בכך אם תנגנו צמדי צלילים אלה בפסנתר). מרווח כזה בין שני צלילים נקרא בשם "קְוִינטה" (מלשון 5, משום שהצליל הגבוה יותר נמצא 5 טונים מעל הנמוך. כך, למשל, "סול" בא במקום החמישי אחרי "דו": דוֹ, רֶה, מי, פָה, סוֹל).
צירוף הרמוני נוסף הוא צירוף שני צלילים שיַחס התדרים שלהם הוא 4:3, כלומר, תדר הצליל הגבוה מביניהם גבוה פי 4/3 מתדר הצליל הנמוך. צלילים כאלה מרוחקים זה מזה 5 חצאי טונים. למשל הצלילים "דוֹ" ו-"פָה", או צמד הצלילים "רֶה" ו-"סוֹל". המִרווח בין שני צלילים כאלה נקרא בשם "קוורטה" (מלשון 4, מאחר שהצליל הגבוה יותר נמצא במקום הרביעי מהנמוך, למשל: "פָה" ו-"דו": דו, רה, מי, פָה). מִרווח הרמוני נוסף, המכונה "טרצה" (מלשון 3), כולל 2 צלילים שיחס התדרים ביניהם הוא 5/4 , כלומר תדר הצליל הגבוה יותר הוא פי 5/4 מתדר הצליל הנמוך. למשל, המרווח בין "דו" ל-"מי", או בין "סול" ל-"סי" הוא טרצה. הרווח בין שני צלילים כאלו הוא 4 חצאי טונים (טבלה א).
| טבלה א | על מרווחים והרמוניות | ||||
| טרצה | קוורטה | קוינטה | אוקטבה | מרווח |
|
5:4 |
4:3 |
3:2 |
2:1 |
יחס תדרים |
|
4 |
5 |
7 |
12 |
מרחק בחצאי טונים בין הצלילים |
יש להדגיש שבכל צירוף הרמוני נוכל לבחור בצליל ראשון כלשהו, כשהצליל השני נקבע על פי המרווח בין הצלילים המתאים להרמוניה המבוקשת. למשל, אם הצליל הראשון הוא "מי" אזי הקוִינטה שלו "סי" (המרוחק 7 חצאי צלילים מ-"מי"), והטרצה שלו "סול דיאז" המרוחק 4 חצאי טונים ממנו.
 |
פעימות וסולמות |
שתי שאלות יסודיות עולות מכך. ראשית: מדוע צירוף שני צלילים שיחס התדרים שלהם הוא כיחס בין שני מספרים שלמים קטנים הוא צירוף הרמוני נעים לאוזן? התשובה לכך נעוצה בעובדה שכאשר אנו מפיקים צליל מכלי נגינה מסוים, למשל גיטרה או כינור, הצליל איננו "נקי". הוא כולל קבוצה גדולה של צלילים עיליים (Overtones) שעוצמתם פוחתת והולכת ביחס לצליל היסודי. כך למשל כאשר משמיעים את הצליל "דו" בגיטרה, צליל זה כולל גם את "דו-אוקטב" (= דו הגבוה באוקטבה אחת, דהיינו: שתדירותו כפולה) וכן את "סול-אוקטב", ועוד שורה ארוכה של צלילים. הפיזיקה מלמדת אותנו שהיחס בין התדרים של הצלילים העיליים לבין הצליל היסודי עצמו הוא יחס מספרי פשוט. לפיכך, כאשר משמיעים יחד שני צלילים שיחס התדרים שלהם הוא הרמוני, כמו 3:2, הצליל הגבוה מבין השניים מתלכד עם אחד הצלילים העיליים של הצליל הנמוך יותר, ומגביר את עוצמתו, וכך צירוף שני הצלילים ערב לאוזן. הֶסבר פיזיקלי זה אינו שלם, מכיוון שאין בכוחו להסביר את התחושה הנעימה כחוויה, ואולם התיאור המתמטי של הצלילים מאפשר לברור מבֵּין האוסף העצום של נתונים קוליים המגיעים לאוזנינו את אלה שיש בכוחם לגרום לנו הרגשת נעימות, אם כי איננו מבינים די הצורך את הסיבות לכך.
ומדוע צירוף שני צלילים שיחסם אינו הרמוני צורם? הפיזיקאי והפיזיולוג הלמהולץ ייחס את הסיבה לכך להיווצרות "פעימות" (beats) בין שני צלילים שיש להם תדר קרוב זה לזה. אם תפְרטו יחד על שני מיתרים בגיטרה שיש להם צלילים מאד קרובים, תשמעו כעין פעימות המהוות "רעש רקע" הפוגם בהנאה.
קיימות שאלות מעניינות נוספות הקשורות לסולם המוזיקלי: מדוע חולקה האוקטבה במוזיקה המערבית ל-12 צלילים דווקא? מה קובע את יחס התדרים בין צליל בסולם לצליל הבא אחריו, הגבוה ממנו בחצי טון (למשל, יחס התדרים בין "דו" ל-"דו דיאֶז" או בין "מי" ל"פָה")? לשאלות אלו יש טעם, בין היתר מכיוון שקיימות תרבויות מוזיקליות בהן האוקטבה חולקה ל-5 חלקים (הסולם הפנטפוני), למשל המוזיקה במזרח הרחוק. התשובות לשאלות הללו קשורות למה שמכונֶה במוזיקה "מעגל הקוִינטות". מסתבר ששתי הרמוניות מספיקות כדי להגדיר את כל 12 הצלילים בסולם המערבי, והן האוקטבה (יחס 2:1) והקוִינטה (יחס 3:2). אם נצא מצליל יסודי מסוים, נניח "דו", בעזרת היחסים הללו ניתן לקבל (כמבואר בתיבה: סולם מעגל הקוִינטות) את כל 12 הצלילים של הסולם המוזיקלי המתחיל בצליל "דו" (טבלה ב).
| טבלה ב | הסולם המתקבל על פי מעגל הקוינטות | |||||||||||||
|
דו-אוקטב (בערך) |
סי |
לה דיאז |
לה |
סול דיאז |
סול |
פה דיאז |
פה |
מי |
רה דיאז |
רה |
דו דיאז |
דו |
צליל |
|
1059 |
992 |
942 |
882 |
837 |
784 |
744 |
706 |
661 |
628 |
588 |
558 |
523 |
תדר בהרץ |
 |
סולם מעגל הקוינטות |
התדר המתאים לצליל "דוֹ" הוא 523 הֶרץ. האוקטבה שלו היא 1046 = 2x523 הרץ. הקוִינטה שלו:  - תדר המתאים לצליל "סוֹל". תדר הקוינטה של f3 הוא
- תדר המתאים לצליל "סוֹל". תדר הקוינטה של f3 הוא 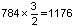 , ואולם תדר זה גבוה מתדר דוֹ-אוֹקטב (1046). על כן נחלק זאת ב-2, כדי למצוא את הצליל הנמוך באוקטבה מהצליל בעל התדר 1176, ונקבל:
, ואולם תדר זה גבוה מתדר דוֹ-אוֹקטב (1046). על כן נחלק זאת ב-2, כדי למצוא את הצליל הנמוך באוקטבה מהצליל בעל התדר 1176, ונקבל: 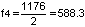 - תדר זה מתאים לצליל "רֶה". הצליל הבא יהיה מרוחק קוינטה מ- f4 כלומר,
- תדר זה מתאים לצליל "רֶה". הצליל הבא יהיה מרוחק קוינטה מ- f4 כלומר, 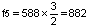 , המתאים לצליל "לָה" הנמצא 7 חצאי טונים מעל "רה".
, המתאים לצליל "לָה" הנמצא 7 חצאי טונים מעל "רה".
באופן זה נמשיך: 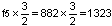 . מכיוון שתדר זה גבוה מהתדר דוֹ-אוקטב (1064), נחשב את הצליל הנמוך ממנו באוקטבה ונקבל
. מכיוון שתדר זה גבוה מהתדר דוֹ-אוקטב (1064), נחשב את הצליל הנמוך ממנו באוקטבה ונקבל 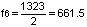 , המתאים לצליל "מי" הנמצא 7 חצאי טונים מעל "לה". אם נמשיך בחישוב כזה 12 פעם נגיע בסופו של התהליך לצליל שהתדר שלו מתאים בערך לתדר הצליל דוֹ-אוקטב. על כן, אם בונים סולם על פי מעגל הקוִינטות הוא יכיל את 12 הצלילים, כפי שנראה בטבלה:
, המתאים לצליל "מי" הנמצא 7 חצאי טונים מעל "לה". אם נמשיך בחישוב כזה 12 פעם נגיע בסופו של התהליך לצליל שהתדר שלו מתאים בערך לתדר הצליל דוֹ-אוקטב. על כן, אם בונים סולם על פי מעגל הקוִינטות הוא יכיל את 12 הצלילים, כפי שנראה בטבלה:
| . | |||||||||||||
|
דו-אוקטב |
פה |
לה דיאז |
רה דיאז |
סול דיאז |
דו דיאז |
פה דיאז |
סי |
מי |
לה |
רה |
סול |
דו |
צליל |
|
1059 |
706 |
942 |
628 |
837 |
558 |
744 |
992 |
661 |
882 |
588 |
784 |
523 |
תדר |
סידור הצלילים לפי סדר התדרים יצר את הסולם המתקבל על פי מעגל הקוִינטות (טבלה ב).
 |
שלבים בסולם |
לסולם המוזיקלי הזה יש חסרונות. למשל, היחס בין שני צלילים סמוכים בסולם אינו קבוע4. אמנם, ההפרש בין היחסים אינו גדול, ועל כן כשכיוונו את כלי הנגינה על פי מעגל הקוִינטות חיסרון זה כמעט שלא הורגש. ואכן, סולם זה היה מקובל עד תקופתו של יוהאן סבסטיאן באך. זה היה סולם נוח, מכיוון שגם ההרמוניות האחרות, כמו טרצה וקוורטה, התקיימו בו5. יחד עם זאת, התעוררו בעיות: למשל, היחסים בין התדרים של שני חצאי טונים סמוכים לא היו קבועים. כתוצאה מכך, בכלִי נגינה הבנוי לפי סולם זה מידת הדיוק בהרמוניות תלויה בצליל היסודי של הסולם. על כן יתכן בהחלט שהרמוניות ישמעו "נקיות" יותר בסולם "דו" מאשר בסולם המתחיל ב"רֶה". וכן, ביצירות מוזיקליות רבות קיימים מעברים בין סולם אחד לשני (מעברים שהמוזיקאים מכנים מוֹדוּלציות), כן שאם היצירות הללו מנוגנות בכלֵי נגינה שנבנו על פי מעגל הקוִינטות, המעברים הללו עלולים להישמע צורמים.
 |
סולמו של גאון |
הבעיות הללו הניעו את המוזיקולוגים לנסות ולשכלל את אופן החישוב של צלילי הסולם, ולהעמיד אותו על בסיס אחיד יותר. לצורך זה השתמש יוהאן סבסטיאן באך בשיטת ה"איזון המושווה" וחיבר יצירה לפסנתר שנועדה להדגים זאת, אותה כינה "הפסנתר המושווה היטב"6. הרעיון היה מבוסס על ההנחה שהיחס בין התדרים של כל שני צלילים סמוכים בסולם חייב להיות קבוע. אם נסמן יחס זה באות r, ואת תדר הצליל היסודי בסולם באות f0 אזי תדר הצליל השני יהיה f1=r*f0, תדר הצליל השלישי יהיהf2=r*f1=r2*f0, וכך הלאה. מאחר שהצליל ה-12 הוא האוקטב של הצליל היסודי, ערכו צריך להיות 2f0 ולכן: r12*f0=2f0. בחישוב קל מתברר כי ערכו של r הוא 1.05946. על פי יחס זה נבנית טבלת תדרים לסולם המוזיקלי המתחיל בצליל דוֹ בשיטת ה"איזון המושווה" (טבלה ג). תדר כל צליל בטבלה זו גבוה פי 1.05946 מהצליל הקודם לו.
| טבלה ג | סולם האיזון המושווה | |||||||||||||
|
דו |
סי |
לה דיאז |
לה |
סול דיאז |
סול |
פה דיאז |
פה |
מי |
רה דיאז |
רה |
דו דיאז |
דו |
צליל |
|
1046 |
987 |
932 |
880 |
830 |
784 |
740 |
698 |
659 |
622 |
587 |
554 |
523 |
תדר |
בסולם המתקבל בשיטת האיזון המושווה יחס התדרים בין כל שני צלילים סמוכים בו הוא, כאמור, קבוע, ולהרמוניות דיוק רב יותר7. על כן שיטת האיזון המושווה עדיפה על מעגל הקוינטות לצורך בניית הסולם המוזיקלי. מאחר שבשיטה זו יחס התדרים בין שני צלילים עוקבים הוא קבוע, איכות ההרמוניות בלתי תלויה בצליל היסודי של הסולם ואינה נפגעת במודולציות.
 |
מזרח/מערב = 12/5 |
האם ניתן להגדיר סולם מוזיקלי שמספר הצלילים שבו יהיה שונה מ-12 ועדיין תישמרנה בו ההרמוניות? נניח שאנו מחלקים את האוקטבה למספר כלשהו (n) של חלקים, כך שהיחס בין התדרים של כל שני צלילים הוא קבוע: r. יחס התדרים של הצליל השני לראשון יהיה r, יחס התדרים בין הצליל השלישי לראשון יהיה r2 וכן הלאה. בעזרת חישוב בסיסי מתברר כי בסולם המכיל 5 צלילים, יחס הקוינטה מתקבל בדיוק טוב (1.5157) וגם יחס התדרים 4/3 המתאים לקוורטה מתקבל בדיוק דומה (1.3195), אך יחסי התדרים הטובים ביותר עבור שלוש ההרמוניות – הקוינטה, קוורטה וטרצה – מתקבלים בסולם הכולל 12 צלילים. רואים, איפוא, שאם רוצים לבנות סולם מוזיקלי בו מתקבלות שלוש ההרמוניות היסודיות ברמת דיוק גבוהה ביותר, יש לחלק את האוקטבה ל-12 חלקים. אם מסתפקים בשתי הרמוניות, האוקטבה והקוורטה, הרי גם סולם הכולל 5 צלילים טוב למדי.
מתעוררת השאלה: האם קיים סולם הכולל n צלילים כך שיַחס הקוִינטה 3/2 מתקבל בו במדוייק? מניתוח מתמטי מסתבר שהתשובה לכך היא שלילית: לא קיים מספר n כזה בו ההרמוניה 3/2 מתקבלת במדוייק. אם כך ראוי לשאול: עבור אילו ערכים מתקבלות ההרמוניות בקירוב הטוב ביותר? נוכחנו כבר כי בטווח המספרים 2 עד 12 המספרים הטובים ביותר הם 5=n ו-n=12. אם נרחיב לערכים גדולים מ-12 ייתברר כי הרמוניות מתקבלות בדיוק טוב מאד גם עבור n=41, n=53. מובן מאליו שכאשר מגדילים את מספר הצלילים (n) בסולם, ההפרש בין יחסי התדרים של שני צלילים סמוכים קטן והולך, כך שהסבירות לקבלת ההרמוניות 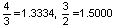 ו-
ו- 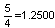 גדלה. סולם המכיל מספר גדול של צלילים, למשל 100 צלילים, ניתן למימוש (כינור יכול להפיק צלילים בתדר כלשהו בטווח מוגדר), אך השאלה האם אמנם ייתכן סולם מוזיקלי בן 100 צלילים שייכת לתחום הקוגניציה.
גדלה. סולם המכיל מספר גדול של צלילים, למשל 100 צלילים, ניתן למימוש (כינור יכול להפיק צלילים בתדר כלשהו בטווח מוגדר), אך השאלה האם אמנם ייתכן סולם מוזיקלי בן 100 צלילים שייכת לתחום הקוגניציה.
הסולם הפנטפוני, המכיל חמישה צלילים, משמש כאמור במוזיקת המזרח, בעוד הסולם המכיל 12 צלילים הוא כאמור הסולם הרווח במוזיקה המערבית.
היו מוזיקולוגים שבנו את הסולם המכיל 41 צלילים, והצליחו לחבר יצירות פשוטות בסולם כזה. ואולם ראינו שככל שמספר הצלילים בסולם גדל, ההפרש בין שני צלילים סמוכים קטן; אם הפרש זה קטן מערך סף מסוים לא ניתן להבחין בין הצלילים הסמוכים. כמו כן הסתבר שסולם בו הרווחים בין הצלילים קטנים מאד ביחס לרווח של חצי טון לא הניב מוזיקה השונה באופן מהותי מזו המוכֶּרת במערב. מעניין לציין כי האדם (לאמור – המוזיקאים) הגיע לשני הסולמות האופטימלים מבחינה הרמונית – סולם פנטפוני וסולם כרומטי המכיל 12 צלילים – לא על סמך ניתוח מתמטי-תיאורטי, אלא בתהליך של ניסוי ותעיה, המאפיין הרבה תהליכים אבולוציונים. הניתוח התיאורטי מצדיק, בדיעבד, באופן מתמטי, את ההתפתחות הטבעית של הסולם המוזיקלי.
היו תרבויות רבות בהן ההרמוניה לא שיחקה תפקיד בהתפתחותם המוזיקלית מכיוון שלא היה בהן מקום מיוחד לזמרה במקהלה, או למוזיקה רב-צלילית (פוליפונית) בה מנגנים מספר כלי נגינה באותו הזמן. ואכן תרבויות אלו פיתתו מערכת סולמות אחרת, למשל הסולמות הרווחים במוזיקה הערבית או ההודית.
 |
על עצב ועל גוון |
ניתן לבנות סולמות שלא על פי האיזון המושווה. דוגמה אחת לכך היא הסולם המבוסס על מעגל הקוינטות. דוגמה אחרת הוא הסולם הפנטפוני הכולל 5 צלילים, הסולם הרווח במוזיקה של המזרח הרחוק. צלילי סולם זה מתקבלים בפריטה על הקלידים השחורים בפסנתר החל מ-פה דיאז (הצלילים: פה-דיאז, סול-דיאז, לה-דיאז, דו-דיאז ו-רה-דיאז). אמנם, סולם זה כולל את ההרמוניות קוינטה וקוורטה, אך אין אפשרות להתחיל את הסולם בכל אחד מהצלילים שבו. כך למשל, אם מתחילים את הסולם בצליל השני שלו, (סול-דיאז) מתקבלת נעימה שונה לחלוטין. כך גם בסולמות הדיאטוניים המחלקים את האוקטבה למספר מסויים של טונים וחצאי טונים על פי חוקיות הנקבעת על ידי מתכנן הסולם. למשל, הסולם הכולל את כל הקלידים הלבָנים בפסנתר ומתחיל בצליל דו (סולם זה ידוע בשם דו-מָג'וֹר). אם נתחיל את הסולם הזה בצלילו השני (רה) נקבל נעימה שונה לחלוטין (זה סולם רה-מינוֹר, הנושא אופי יותר "עצוב"). הסולמות היחידים בהם המוזיקה אינה תלוייה באיזה צליל בסולם מתחילים הם הסולמות הבנויים על בסיס עקרון האיזון המושווה; כאמור, רק בסולמות כאלה ניתן לעבור מסולם לסולם (לבצע מודולציות) ללא חשש בפגימת ההרמוניות.
ומשהו על גוון הצליל. כיצד אנו יכולים לדעת האם מקור צליל מסוים הוא כינור או חצוצרה? מסתבר שהתכונה הפיזיקלית המאפיינת את גוון הצליל קשורה קשר אמיץ לצלילים העיליים שלו. נוכחנו כי כל צליל המופק מכלי נגינה מאופיין על ידי צליל יסודי וצלילים עיליים שתדירותם היא מכפלה של מספר שלם בתדר הצליל היסודי. מה שמבחין בין כלֵי נגינה שונים הן העוצמות היחסיות של הצלילים העיליים הללו. לכל כלי נגינה ולכל צליל המופק ממנו יש כעין "תעודת זהות" המוגדרת על ידי היחס בין העוצמות (החוזק) של הצלילים העיליים לעוצמת הצליל היסודי. האורגנים האלקטרוניים מנצלים עובדה זו כדי להפיק צלילים של כלי נגינה שונים על ידי הפקה של צלילים עיליים התואמים כל כלי נגינה מבוקש.
מובן שהיופי הכמוס ביצירות מוזיקליות אינו ניתן למיצוי בסולם הצלילים ובהרמוניות הנוצרות מהם. היצירתיות המוזיקלית הבאה לידי ביטוי בצירוף הצלילים ליצירה אינה ניתנת להעמדה על בסיס מתמטי. יחד עם זאת, גם במבנים מוזיקליים יש רכיבים כמותיים התורמים תרומה חשובה ליופי שביצירה. כך, למשל, במספר ניכר של יצירות מוזיקליות, כמו בפוּגוֹת של יוהאן סבסטיאן באך, ישנם קטעים המהווים "כפילים" כמעט סימטריים של קטעים אחרים. הסימטריה משחקת איפוא תפקיד מרכזי ביותר, לא רק בתיאור המציאות הפיזיקלית המַקרוסקופית (כמו בגבישים) והמיקרוסקופית (בתיאוריות ה"סופרסימטריה" לכוחות וחלקיקים יסודיים בטבע), אלא גם באמנויות (למשל בעבודותיו של אֶשֶׁר), וכפי שנוכחנו – גם במוזיקה. על הקשר בין היצירות של אשר ובאך לבין רעיונותיו של המתמטיקאי בן המאה העשרים קורט גדל, כתב הופשטטר ספר מעניין ביותר שזכה בפרס פוליצר.
הערות שוליים:
- פיתגורס עצמו הפיק את המרווחים מחלוקת אותו מיתר עצמו, שיטה ששמשה במונוכורד, הכלי העיקרי ללימוד התיאוריה המוזיקלית בימי הביניים.
- בימי הביניים נכללה המוזיקה ב-Quadrivium – '"ארבע האמנויות": אריתמטיקה, גיאומטריה, מוזיקה ואסטרונומיה.
- ואולם רוסו התנגד להרמוניה, והדגיש דווקא את ייחודה של כל קבוצה אתנית.
- למשל, יחס התדרים בין "דוֹ-דיאֶז" ל-"דוֹ" הוא:
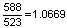 ואילו היחס בין "רֶה" ל-"דו-דיאז" הוא:
ואילו היחס בין "רֶה" ל-"דו-דיאז" הוא: 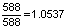 .
. - כך למשל, יחס הצלילים בין "פה" ל-"דו" הוא:
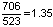 קרוב מאד לקוורטה
קרוב מאד לקוורטה 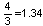 ויחס הצלילים בין "מי" ל-"דו"
ויחס הצלילים בין "מי" ל-"דו"  קרוב מאד לטרצה 1.25 = 5:4.
קרוב מאד לטרצה 1.25 = 5:4. - למעשה, השיטה המושווית הוצעה על-ידי ז'אן-פיליפ ראמו (Rameau 1683-1764), מוזיקאי ומוזיקולוג צרפתי. ראמו נתן בזמנו את ההסבר החדשני ביותר לקשרים שבין מוזיקה, מתמטיקה ופיזיקה. י. ס. באך, בן דורו של ראמו, לא המציא את השיטה המושווית, אלא עשה בה שימוש. המונח המקורי של באך הוא Wohltemperierte שפירושו "ממוזג היטב".
- נבדוק, למשל, את יחס הקוינטה: יחס התדרים בין "סול" ל-"דו"
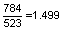 שווה בקירוב טוב מאד ל-
שווה בקירוב טוב מאד ל- 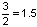 וכך גם היחס בין "לה" ל-"רה"
וכך גם היחס בין "לה" ל-"רה" 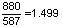 גם יחס הקוורטה מתקבל בדיוק טוב מאד, למשל: יחס התדרים בין הצלילים "פה" ל-"דו" הוא:
גם יחס הקוורטה מתקבל בדיוק טוב מאד, למשל: יחס התדרים בין הצלילים "פה" ל-"דו" הוא: 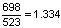 .
.
לקריאה נוספת:
- שושני: מחשבות על התבונה, יצא לאור בקרוב בספריית ה"אוניברסיטה המשודרת", משרד הביטחון – ההוצאה לאור.
- דליה כהן, אקוסטיקה ומוסיקה, הוצאת אקדמון, 1983.
- The Oxford Dictionary of Music, 2nd Edition, Editor: Michael Kennedy, Oxford University Press, 1994.
- D. R. Hofstadter: Godel, Escher, Bach; An Eternal Golden Braid, 20th Edition, Basic Books, 1999.
| ביבליוגרפיה: | ||||||||||||
|
 |
 |
חזרה3 |
 |
הדפסה | ||||||
| החומר במאגר זה הינו לשימוש פרטי ולשימושם של מורים ותלמידים לצרכים לימודיים בלבד. אין להפיץ, להעתיק, לשדר או לפרסם חומר כלשהו מתוך המאגר, ללא הסכמה מראש ובכתב של בעלי זכויות היוצרים השונים, המצויינים בתחתית כל פריט. | |||||||
|
|||||||
| החומר במאגר זה הינו לשימוש פרטי ולשימושם של מורים ותלמידים לצרכים לימודיים בלבד. אין להפיץ, להעתיק, לשדר או לפרסם חומר כלשהו מתוך המאגר, ללא הסכמה מראש ובכתב של בעלי זכויות היוצרים השונים, המצויינים בתחתית כל פריט. |